My niche area:
As an Aerospace Engineer, and more importantly an engineer, it is my duty to convey complex technicalities in layman terms. I worked on my master thesis in the domain of "Aeroacoustics". The subject deals with sound (acoustics) produced by Aerodynamic flow (aero).
The thesis was a part of a EU-H2020 project SmartANSWER, addressing the flow induced acoustic transmission and radiation and working towards it's reduction. Being a sustainable enthusiast, confidently taking steps in solving the current problems with a foresight, I took up Aeroacoustics, a subject which was pretty new. Motivated, I learnt the concepts and simultaneously applied them to make innovative modiciations to my test setup, which was quite complex.
My thesis dealt with the concept of analysing the noise arising from the bypass duct of an aircraft engine. The phenomenon of noise production can be summarised as follows:
The simple physics:
Turbulent (chaotic) flow arising from the engine fan produce noise when they impinge on the nearby static guide vanes (blades). The noise production is caused by what is called as unsteady blade loading, i.e., the force which the blade feels where the turbulent air fows over it. These unsteady force fluctuations (pressure fluctations) are amplified by the presence of the by-pass duct and propage as noise.
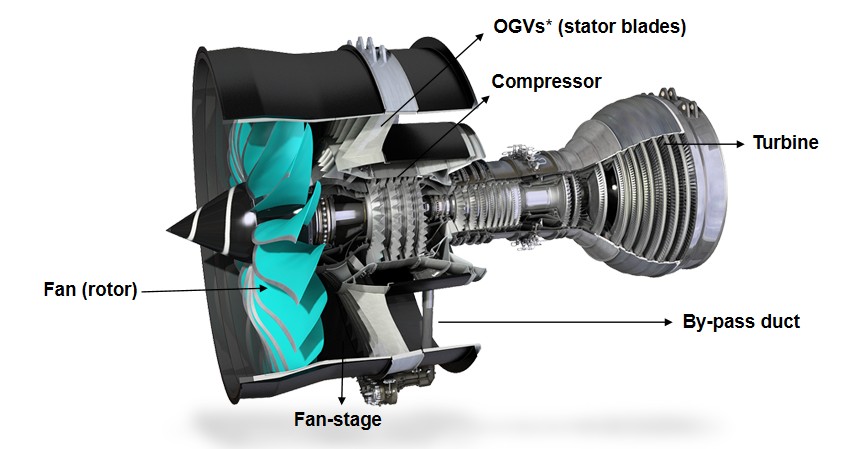
Figure depicting a turbofan engine with by-pass duct; OGVs* (Outlet Guide Vanes)
The main aim of the thesis was to analyze this noise at a component level first, by simplifying the complexity of the engine environment as much as possible. Hence, it was decided to study the vortex cascade interaction noise by using a simple Rod-airfoil configuration.
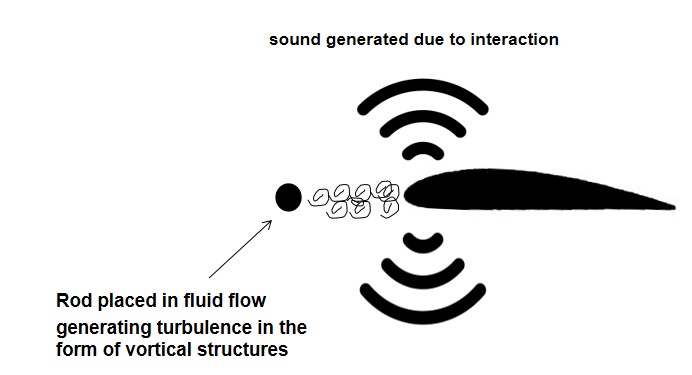
Figure showing a rod-airfoil configuration undegoing in a turbulent-arifoil ineraction setting
So how does this setup differ form a complex engine? By looks, very much, as shown below.
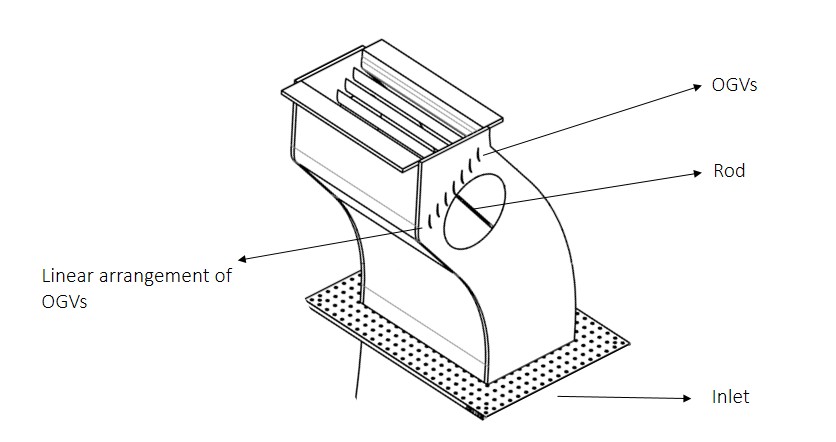
Figure depicting the actual setup which was simplified to a component level
But when it comes to physics, it's pretty similar.
| Complete setup | Simplified setup |
Similar geometrical parameters | Yes | Yes |
Similar flow parameters | Yes | Yes |
Now that you know a bit about the subject, let's dive into the unprecedent problem which occurred during experimentation with the simplified setup.
The problem:
During the root cause analyses, it is important to ensure that the system we are working with is fully functional and upto the standards.
My experiments were performed in a wind tunnel kept in an anechoic room. When I realized that there was a problem with my system, I was mid-way into completing my experiments. I was almost done with my acoustic measurements, and suddenly realized that the wing which I have been using to study the turbulence interaction noise could not handle high loading (high flow speed) and started bending.
But why is wing bending a problem?
- We do not have the same geometrical parameters as desired
- The flow field around the wing gets complicated
- Huge uncertainty in loading and the noise measured is not close to what is expected
I had two possibilities to move forward. The obvious one was to manufacture the wing again with better strength to withstand high loading. But this would've drastically altered my schedule and pushed my graduation by months.
This was a test to my analytical capabilities and I came up with a better way to address the issue.
The approach:
I structured my approach to use the available resources at hand, in an efffective and efficent manner.
- First, I came to the conclusion that I could reduce the size of the wing by reinforcing the corners better. The thing about reinforcing the corners is to reduce the bending of the wing, since a reduction in the length of the wing is proportional to increasing it's stiffness. This "Eureka" moment dawned upon me when I was willing to imporve my knowledge in the subject of structures, to devise a strategy to tackle this issue. I had a good foundation in it from my bachelor's, and I was persistent.
- Next, a reduction in the size of the wing could lead to a reduction in the noise, but this would be a known variable. Now that the stiffness of the wing is better, the noise measured in this setting can be scaled to the actual levels as if the whole wing were exposed to the turbulent flow.
- Although this could solve the problem, it was also pertinent that I account for the possible loss in lift (loading) due to wing bending (unseen to the naked eye) after I proceeded with the above-mentioned steps.
Problem-solving:
I translated the happenings of the experiment analytically into the simplified problem of a simply supported beam. Considering a uniformly distributed load over the wing (due to the uniform flowfield), I derived a formula for calculating the loading which would arise due to a particular maximum displacement of the wing (at the center of the wing).
To understand this better, consider a rope held tightly on both ends. You will notice that the maximum displcement of the rope from it's original position occurs when you hang from it's central location. Now, for the formulation to be complete, it was also necessary to calculate the stiffness the material of the wing.
Now came another question of how I will be able to co-relate the analytical relationship between force and displacement to the actual measurements. I had what was called as the load cell (measures the loading on the wing), but I needed something to measure the displacement undergone by the wing. I came across a laser which calculates the distance between walls in a room and used the same to calculate the bending of my wing to a mm accuracy. With this ingenious setup, I was able to make a calibration curve which could be applied to the measured lift and to account for the loss in lift occuring due to bending.
Let's get into the actual math involved, it's quite simple and interesting, it's rocket science!!!
The analysis:
The first step in the analysis was to experimentally estimate the stiffness of aluminium, ’EI’. A known set
of weights are placed on one end of a string suspended on a pulley. the other end is attached to the mid-span of the wing. This situation mimics that of a simply supported beam, which gives us the formulation of a point load as,
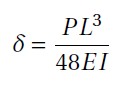
where δ is the displacement (in m), P is the point load (in N) and EI is the stiffness of the material of the
wing. The displacement upon loading is measured using a laser source, whose error in measurement is ± 1 mm.

Figure (a) showing the setup for estimating EI
The laser source (not shown in Figure a) is placed at a reference distance. Upon loading,
the wing bends, and this distance is recorded by the laser sources, the difference between the two being the δ. The measured displacements and the corresponding loads are tabulated in table A.1, and the average EI is estimated to be 4.884 N/m.
The second step is accounting for wing bending analytically as explained before. This is done by considering a uniformly distributed load over a simply supported beam, where the load distribution is imparted only to the wetted region (region under the influence of flow), 250 mm.
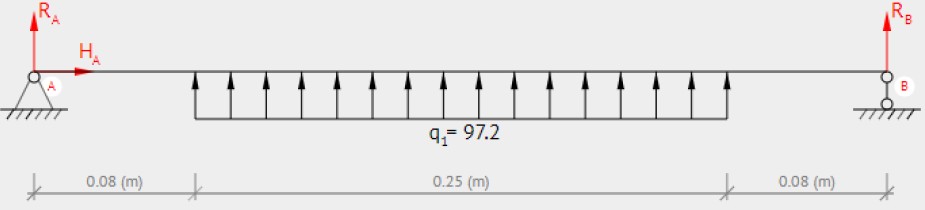
Figure b : Schematic of the load distribution over the wing for analytical formulation
q1, as shown in figure b refers to the UDL, in N/m. According to the second order differential equation
for elastic curve of a beam deflection,
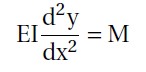
where M is the bending moment and y is the deflection of the beam. Solving this equation using boundary conditions which specify that deflection is 0 at both ends, the formulation obtained was

where b is the distance of the beam which is loaded (0.25m in this case), a is the distance which is not
loaded (0.08mfor this case) and L is the overall length of the beam. A calibration curve was then constructed relating the force measured by the load cell and the force expected from the analytical formulation, where the input is the δ max measured by the laser cell. The wind tunnel was turned on and the data obtained is shown below:
Velocity | Displacement measured (in m) | Force using analytical formula (N) | Force (in Kg) | Force measured by load cell |
20 | 1 | 4.88 | 0.498 | 2.25 |
30 | 1 | 4.88 | 0.498 | 4.82 |
40 | 2 | 9.76 | 0.994 | 8.28 |
50 | 3 | 14.64 | 1.492 | 12.82 |
55 | 3 | 14.64 | 1.492 | 15.87 |
58 | 4 | 19.52 | 1.989 | 17.23 |
The calibration curve hence constructed is shown below:
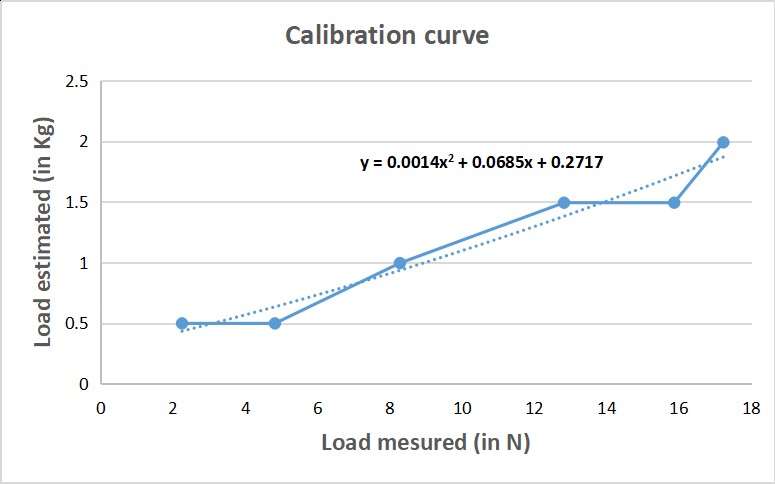
fitting a polynomial of order 2 gives the equation of the curve as
y = 0.0014x2+ 0.07x +0.277
Concluding remarks:
By using this calibration curve to correct for the lift measured, the possible loss in lift was accounted for. Patience and persistence played vital roles in this analysis. It was important to have a fresh mindset to think of ingenious methods. Having a discipline in structuring the approach was crucial to efficently tackle the situation at hand