Introduction
This article focus on forecasting hourly electric loads for the next whole year given clean historical loads records and temperature data. The goal is to find the champion model that provides most accurate forecasts with the help of extensive feature engineering work.
Data
Data has 4 fields and 35,064 observations. Four columns of variables: date, hour, temperature and load. Load history ranges from the 1st hour of 2008/1/1 to the 24th hour of 2011/12/31, while temperature history ranges from the 1st hour of 2008/1/1 to the 24th hour of 2012/12/31. The goal is to forecast the hourly load demand from the 1st hour of 2012/1/1 to the 24th hour of 2012/12/31 given the temperature.
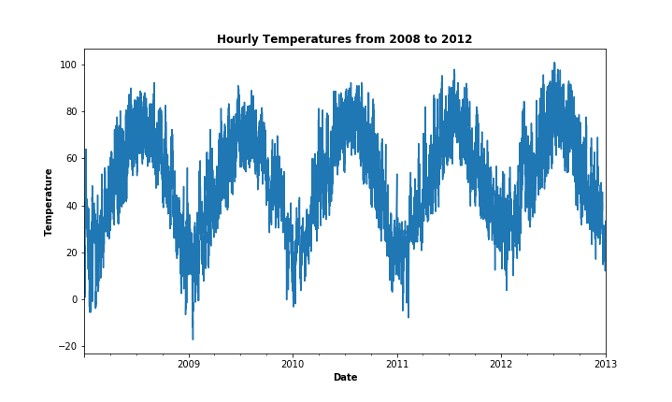
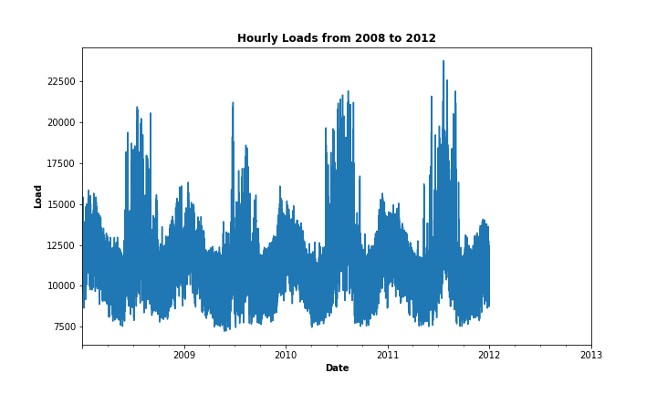
It's unrealistic to have future temperature data available when we are doing forecasting in practice. However, this is a simplified task that help us focus on feature engineering and model tuning.
Feature Engineering
Since only 3 variables are given by the original dataset, more variables are definitely needed to expand the feature space. Hong et al. (2015) captured the missing salient features by including the temperature variables, namely lagged hourly temperatures and 24-hour moving average temperatures. On top of that, Wang et al. (2016) create more features that model the recency effect at an aggregated level. I followed their approach and varied the number of days from 0 to 7, and the number of lags from 0 to 72. In total, 795 variables were created.
data = read_excel("data.xlsx")
# boxlam - BoxCox.lambda(data$Load)
# data$boxload - BoxCox(data$Load, lambda = boxlam)
# create variables like Trend, Month, Weekday, and polynomial and interaction terms
data$weekday = as.POSIXlt(data$Date)$wday+1
data$month = month(ymd(data$Date))
data$trend = c(1: length(data$Date))
data$WH = data$weekday*data$Hour
data$TP2 = data$Temperature**2
data$TP3 = data$Temperature**3
data$TM = data$Temperature*data$month
data$TP2M = data$TP2*data$month
data$TP3M = data$TP3*data$month
data$TH = data$Temperature*data$Hour
data$TP2H = data$TP2*data$Hour
data$TP3H = data$TP3*data$Hour
# create lag temperature variables
data = setDT(data)[, paste0('T', 1:72) := shift(Temperature, 1:72)][]
# create lag polynomial temperature variables
for (i in c(1:72)){
data = setDT(data)[, paste0('T',i,'P2') := '^'(data[[paste0('T',i)]], 2)][]
data = setDT(data)[, paste0('T',i,'P3') := '^'(data[[paste0('T',i)]], 3)][]
}
# create lag month and lag hour variables
data = setDT(data)[, paste0('M', 1:72) := shift(month, 1:72)][]
data = setDT(data)[, paste0('H', 1:72) := shift(Hour, 1:72)][]
# create lag interaction terms
for (i in c(1:72)){
data = setDT(data)[, paste0('T',i,'M',i) := data[[paste0('T',i)]]*data[[paste0('M',i)]]][]
data = setDT(data)[, paste0('T',i,'P2M',i) := data[[paste0('T',i,'P2')]]*data[[paste0('M',i)]]][]
data = setDT(data)[, paste0('T',i,'P3M',i) := data[[paste0('T',i,'P3')]]*data[[paste0('M',i)]]][]
data = setDT(data)[, paste0('T',i,'H',i) := data[[paste0('T',i)]]*data[[paste0('H',i)]]][]
data = setDT(data)[, paste0('T',i,'P2H',i) := data[[paste0('T',i,'P2')]]*data[[paste0('H',i)]]][]
data = setDT(data)[, paste0('T',i,'P3H',i) := data[[paste0('T',i,'P3')]]*data[[paste0('H',i)]]][]
}
# create Moving Average, Moving Minimum, and Moving Maximum temperature variables
for (i in c(1:49)){
data = setDT(data)[, paste0('TDMA',i) := rowMeans(data[,(10+i):(33+i)])][]
data = setDT(data)[, paste0('TDMin',i) := apply(data[,(10+i):(33+i)],1,FUN=min)][]
data = setDT(data)[, paste0('TDMax',i) := apply(data[,(10+i):(33+i)],1,FUN=max)][]
}
Modeling and Results
Three models are built to forecast the hourly electricity demand for the year 2012.
1. Vanilla benchmark model
The vanilla benchmark model is a multiple linear regression model:
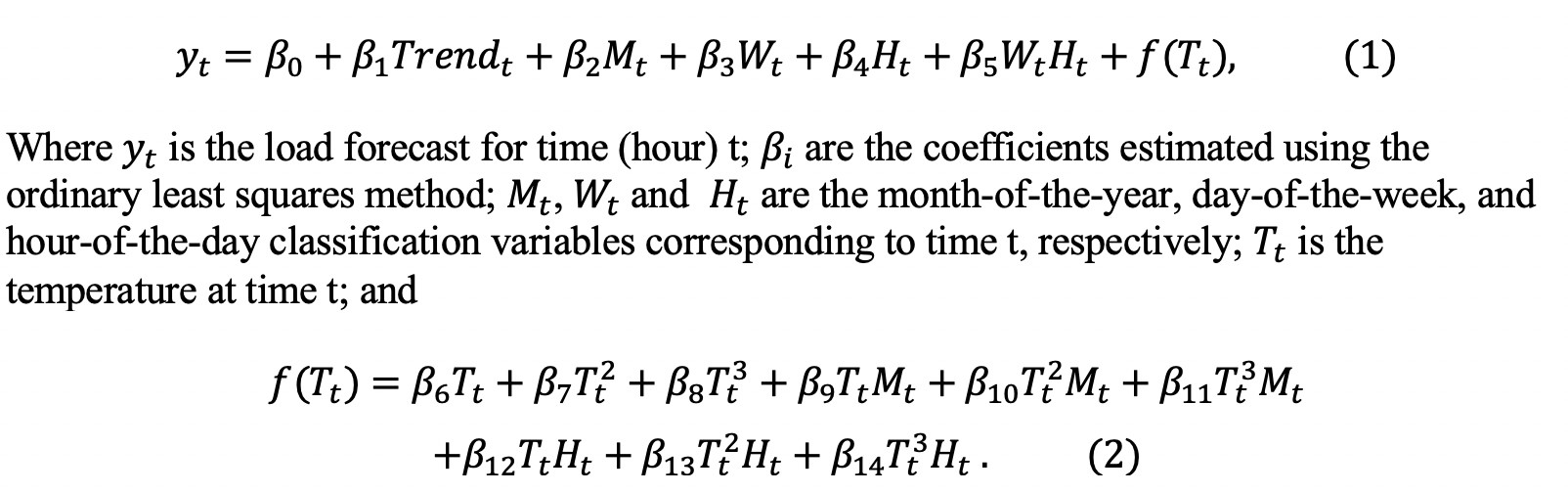
The benchmark model achieves MAPE of 8.92 in training data. The performance is not satisfying even in training dataset. So, an enhanced vanilla model is built on top of that by including created features that model the recency effects at an aggregated level.
2. Enhanced Vanilla Benchmark Model
Wrapping all the created features with a linear model, we get a baseline model that contains ~800 variables:

The multiple linear regression performs better than the vanilla benchmark and achieves a MAPE of 6.0 in training set. MAPEs have decreased a lot by including extra features into the linear model, but still its performance is not very satisfying. So other machine learning models are tried to improve the forecast accuracy.
3. XGBoost
Gradient boosting is a machine learning technique for regression and classification problems, which produces a prediction model in the form of an ensemble of weak prediction models, typically decision trees. Gradient Boosting trains many models in a gradual, additive and sequential manner. Gradient boosting identifies the shortcomings of weak learners by using gradients in the loss function.
The XGBoost achieves best performance among other ML models. I used all the 808 variables built. It achieves a MAPE of 0.66 in train (2018-2010), MAPE of 4.25 in validation (2011), significantly better than the other two models. To improve the model performance, train and validation dataset are combined to train the model.
# xgboost
dtrain = xgb.DMatrix(data = as.matrix(train[,c(2:3,5:232,377:955)]), label=train$Load)
dtest = xgb.DMatrix(data = as.matrix(val[,c(2:3,5:232,377:955)]))
dpred = xgb.DMatrix(data = as.matrix(pred[,c(2:3,5:232,377:955)]))
params = list(booster = "gbtree", objective = "reg:squarederror", eta=0.3, gamma=0, max_depth=6, min_child_weight=1, subsample=1, colsample_bytree=1)
xgbcv = xgb.cv( params = params, data = dtrain, nrounds = 200, nfold = 5, showsd = T, stratified = T, print_every_n = 10, early_stopping_rounds = 20, maximize = F)
bst = xgboost(params = params, data = dtrain, nthread = 2, nrounds = 200,print_every_n = 10, early_stopping_rounds = 10)
xgbpredtrain = predict(bst, dtrain)
MAPE(xgbpredtrain,train$Load) #0.006608219
xgbpredval = predict(bst, dtest)
MAPE(xgbpredval,val$Load) #0.04258473
# retrain using both train and val
dtrain.full = xgb.DMatrix(data = as.matrix(data[1:35064,c(2:3,5:232,377:955)]), label=data[1:35064,]$Load)
bst = xgboost(params = params, data = dtrain.full, nthread = 2, nrounds = 200,print_every_n = 10, early_stopping_rounds = 10)
xgbpred = predict(bst, dpred)
xgbtrain = predict(bst, dtrain.full)
MAPE(xgbtrain,data[1:35064,]$Load)
Conclusion
In this article, I created ~800 variables to model the missing resilient features and the recency effects at an aggregate level. On top of that, three models were built to forecast the hourly electricity loads for the year 2012, and their formance were compared. It's shown that feature engineering plays an critical role in long-term energy demand forecasting. However, correct modeling choice and parameter tuning paired with extensive feature engineering could generate a much better performance.
Reference
[1] Wang, Pu, Bidong Liu, and Tao Hong. "Electric load forecasting with recency effect: A big data approach." International Journal of Forecasting 32.3 (2016): 585-597.
[2] Hong, Tao, Pu Wang, and Laura White. "Weather station selection for electric load forecasting." International Journal of Forecasting 31.2 (2015): 286-295.