Continuing on the last example of weight loss, we keep on diet meals and regular exercise for 100 days. The regression model will tell how much pounds we lose based on pounds of food take in and hours of exercise made. The model learns the best parameter on meal and exercise by considering cost function. By setting up cost function, the model knows how well or bad it performs and adjusts from each training point. This article is summarized based on Andrew NG’s lecture in cost function and gradient descent for study purpose.


Just like human brains, the models learn by changing behaviors to avoid mistakes. We set up the cost function to minimize the gap between the predicted value and observed ones. The cost function below shows θo as intercept on y and θ1 as the slope of the regression line. With these two parameters, we can define any hypothesized line hθ in x-y coordinates. The gap J(θo,θ1) is calculated by taking half of the mean squared difference between each predicted value and observed y(i). By trying out different hypothesized lines, we take the hθ with the smallest gap to approach all real data points.

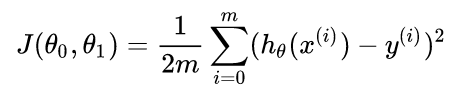
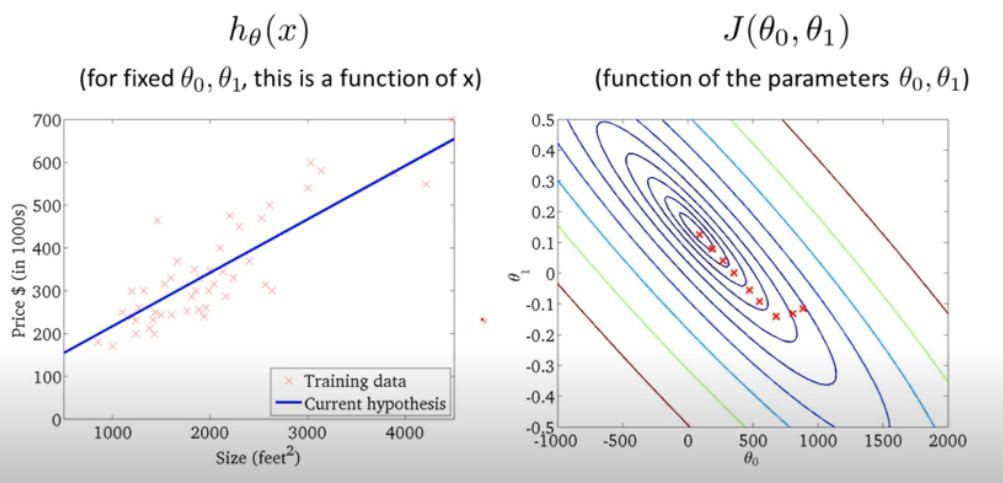
After understanding the calculation process on the cost function, we can map out the cost function with θo and θ1. The lowest point in the graph indicates the best set of θo and θ1.

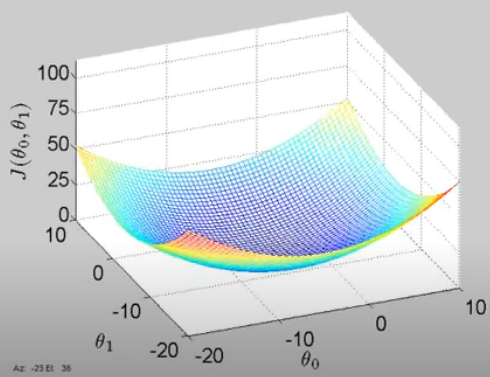
Or we can transfer the plot into 2 dimensions by making a contoured figure, where the center point shows the global minimum of the cost function.

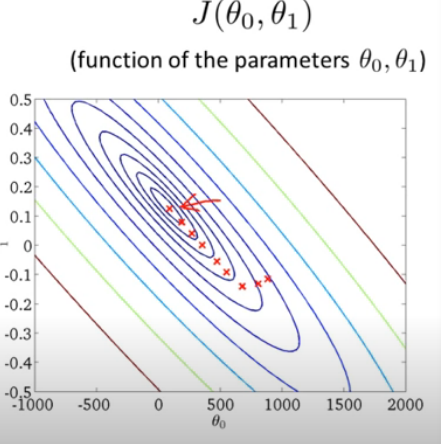
Based on the contour figure, we try to find the global minimum at the center point. Following pictures show how the adjustments are made when linear line is turned around step by step by using all training points in a Batch to assess the cost value J(θo,θ1).

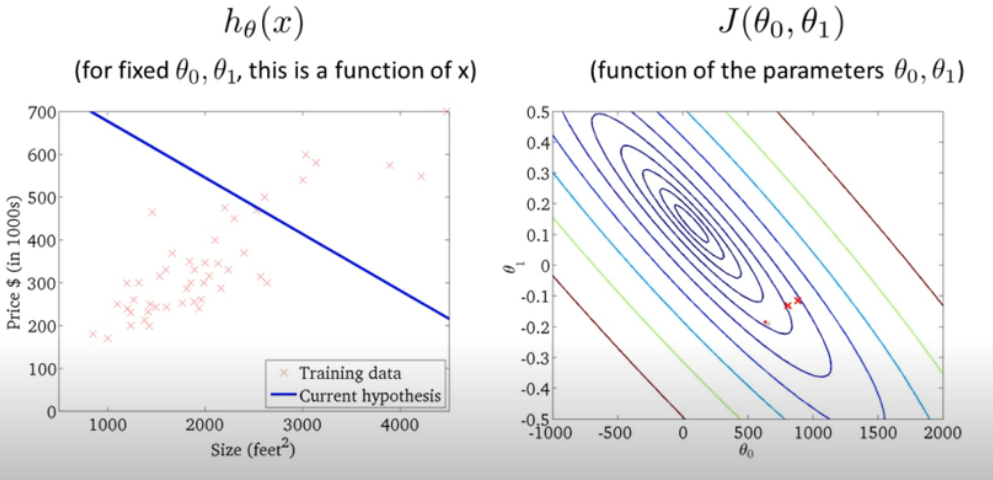

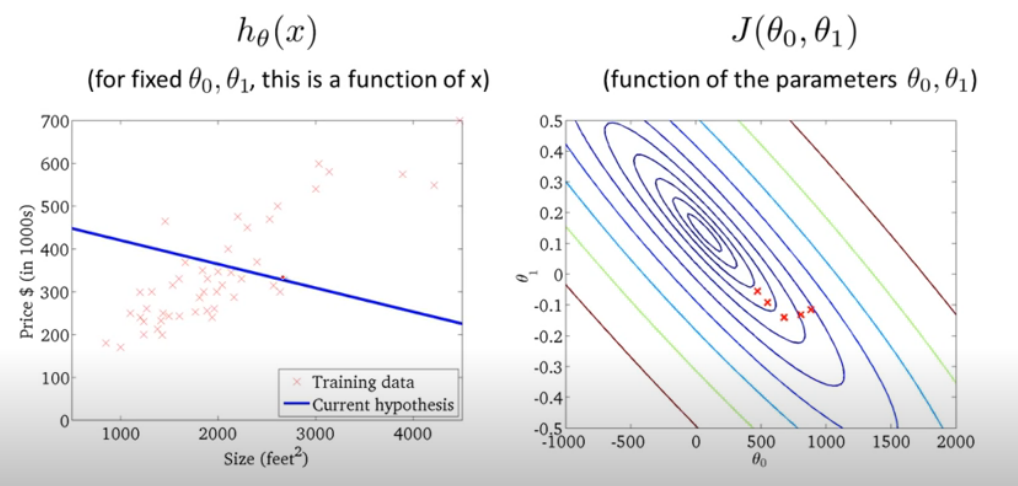

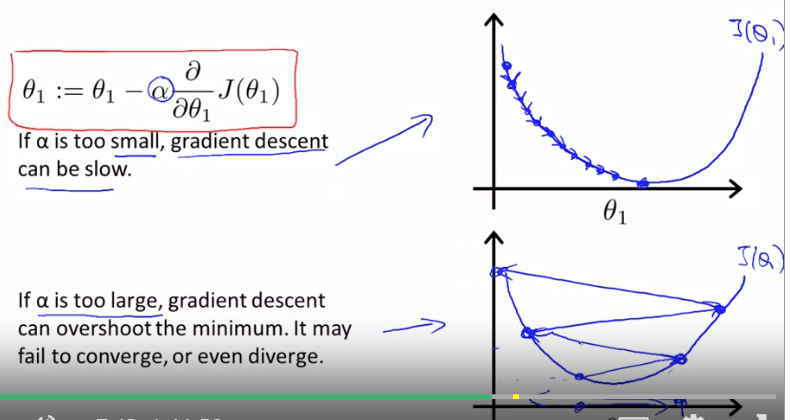
The mathematical way to explain the searching process is by gradient descent algorithm. The intuition is to search with declining slope and to update current (θo,θ1) set by each point. The learning curve, denoted as α , determines how large each step of searching should be.


When approaching a local minimum, gradient descent will automatically take smaller steps even then the learning rate is fixed.
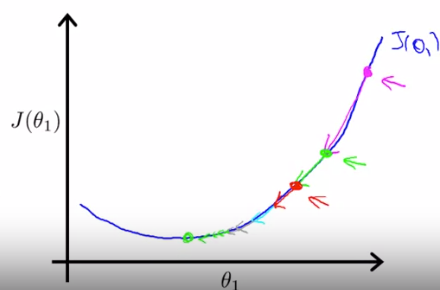
When the searching step is too small or too large, we will miss the optimal solution. But can be trained to find the best fit when tuning hyperparameter.