Introduction:
We are interested in estimating medical costs using various features of patients. Traditionally, a lot of insurance companies use Bayesian networks to do a prediction of medical/auto/home cost to provide insurance services. Also, there has been various research studies on cost prediction using various methods [1,2,3]. In this project, we are interested to use neural networks, where features are a combination of continuous (e.g. age, BMI) and discrete values (e.g. sex). For this reason, we selected a dataset from Kaggle website [4]. Our trained network, has been able to do prediction with low error on the test set. In the following sections, we first explain the technical approach, then we discuss the results and eventually we provide the references.
Technical Approach:
We are using vanilla neural network to train a regression model. To implement the neural network, we are using sequential models of Keras [5] (open source Python library) with TensorFlow backend. The dataset contains 1339 records with 8 features, therefore we expected that a shallow NN would give us reasonable prediction. However, because of small number of records, we were not expecting super accurate results. The hidden layers except the output layer have ReLu activation function and the last layer has linear activation function. We are using Adam optimizer [6] that controls the learning rate. The number of samples per gradient update, also called the batch size is set to the default value of 32. By observation, we found that about 500 epochs would be enough for the training to converge.
Metrics Objective Function:
Given that it’s a regression problem, we have a choice of metrics such as Absolute Mean Square Error (MSE), R-squared, etc.
We are trying to minimize mean squared errors (objective function) and increase R-squared values for our validation set.
Data preprocessing:
One-hot encoding: Since the input data is a combination of discrete and continuous values, we first do one-hot encoding for the categorial features with discrete values such as sex, being a smoker or not and the region where the patient lives.
Normalization: Normalization is a technique often applied as part of data preparation for machine learning. The goal of normalization is to change the values of numeric columns in the dataset to a common scale, without distorting differences in the ranges of values. The features with continuous values in our dataset (bami, age, number of children) are normalized to achieve a common scale.
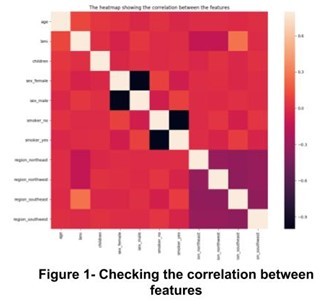
Feature Selection: In order to avoid unnecessary complexity of our model, we examined correlation between the features and since we did not observe any major correlation in the figure below, we kept all the features. Figure 1 shows the correlation heatmap of all features.
Model selection strategy:
To do the model selection, we have two steps:
1- Initially start with 1-fold cross-validation to narrow-down our hyper parameter search. Table 1 has details of all models.
2- Once we have a smaller set of hyper-parameters, we do 5-fold cross-validation among the all possible models associated with the hyper parameters.
One can merge the two steps, but that would increase the computation significantly and the results may not be much different from our approach.
| Hidden Layer 1 |
| Hidden Layer 1 | Hidden Layer 2 |
| Hidden Layer 1 | Hidden Layer 2 | Hidden Layer 3 |
1 | 8 | 5 | 8 | 16 | 9 | 8 | 16 | 32 |
2 | 12 | 6 | 8 | 32 | 10 | 8 | 32 | 16 |
3 | 16 | 7 | 12 | 16 | 11 | 12 | 16 | 12 |
4 | 20 | 8 | 12 | 20 | 12 | 12 | 20 | 8 |
Results and Discussion:
Step 1- Narrowing down the search space
In this step, we test various models with different hidden layers and different number of nodes and plot the loss function of train and test sets. In Figures 2 and 3, the loss function for two networks using test and train sets are plotted. The network with less layers converged faster but with higher loss compared to the network with more layers and nodes.
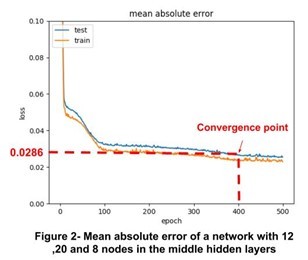
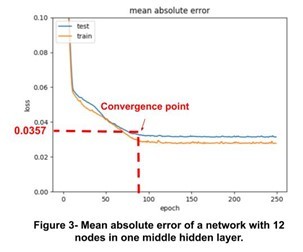
Based on the Figures 2 and 3, we find that using only one hidden layer (total 3 layers), would meet our requirement. In the next step, we are going to discuss the results for 5-fold cross validation.
Step 2: 5-fold cross validation
Using only one hidden layer (total 3 layers), we test various node sizes and do 5-fold cross validation. The results are shown in the Table below :
Number of nodes | Mean Absolute Error | R-Squared |
5 | 0.04576 | 0.6324 |
10 | 0.03567 | 0.6853 |
15 | 0.02356 | 0.7862 |
20 | 0.03895 | 0.7235 |
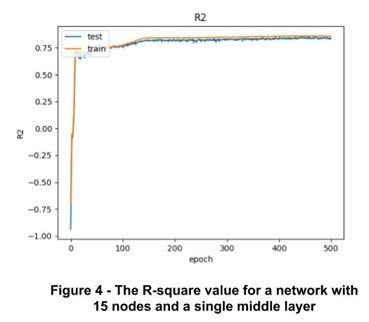
The network with 15 nodes gives us the highest R-squared with 5-fold cross validation. To achieve better performance, we either need more records, or better features such as the disease type, having vaccination or not, etc. Figure 4 shows the plot for R-squared of the selected network with highest performance among all networks that we tried.
Conclusion and Future Work:
In this project, we trained a model that was able make predictions of medical costs for novel patients. For this purpose, we used an artificial neural networks with one hidden layer (3 layers in total). The results showed that the choice of ANN enables us to make predictions successfully. In future, we are interested in having a cost predictor that gets updated iteratively as new data are received from various resources.
References:
[1] Kang, Jin Oh, Suk-Hoon Chung, and Yong-Moo Suh. "Prediction of hospital charges for the cancer patients with data mining techniques." Journal of Korean Society of Medical Informatics 15.1 (2009): 13-23.
[2] Bertsimas, Dimitris, et al. "Algorithmic prediction of health-care costs." Operations Research 56.6 (2008): 1382-1392.
[3] Moran, John L., et al. "New models for old questions: generalized linear models for cost prediction." Journal of evaluation in clinical practice 13.3 (2007): 381-389.
[4] https://www.kaggle.com/mirichoi0218/insurance
[5] Chollet, François. "Keras." (2015).
[6] Kingma, Diederik P., and Jimmy Ba. "Adam: A method for stochastic optimization." arXiv preprint arXiv:1412.6980 (2014).