Application
Handwritten Digit Recognition is to let the computers read the human handwritten digits and convert them into digital form. It is a subset of the Handwritten recognition problem that is commonly used in various applications, including digitizing manuscript documents, reading bank checks, etc. It makes great contributions to the advancement of an automation process and improves the interface between man and machine.
Traditionally, since the handwritten digits are not perfect and can vary depending on the personal styles of individual people, it is hard for the programmers to hard-code the properties of symbols to make the classification. With advancements in the field of deep learning and hardware in the last couple of years however, we can now use neural networks to automatically learn features from analyzing a dataset and then classify images based on weights generated by the learning process. Inititally, the training of neural networks was a slow process however, the advancements in hardware such as the introduction of GPUs, has made that process massively faster. GPUs has now become essential in training neural networks and is used everywhere from research institutions to large corporations.
Although GPUs are widely in use today, in its initial phases that wasn't the case. When GPUs had just become popular in scientific computing some time back in 2001, in order for researchers to code algorithms on the GPU, they had to understand low level graphic processing. It wasn't until 2006, when Nvidia came out with a high level language CUDA, which allowed anyone to write programs for GPUs in a high level language, that GPUs began to be as widely used as today.
The dataset used for the project is the Modified National Institute of Standards and Technology (MNIST) dataset. The MNIST dataset is one of the most common datasets used for image classification and accessible from many different sources. It contains 60,000 training images of handwritten digits from zero to nine and 10,000 images for testing. The images in the dataset are represented as a 28×28 matrix, where each cell contains grayscale pixel value.

In this project, I started with some open-sourced sequential codes of handwritten digit recognition neural networks(https://github.com/HyTruongSon/Neural-Network-MNIST-CPP). The training can be divided into a forward process and backpropagation. I rewrite the sequential codes into CUDA kernels and set the appropriate number of thread blocks and threads per block for each kernel. I allocate memory accessible by the GPU, copy the input training set to it and launch the kernels in order to invoke them on the GPU. Then I can get the weights learned by the training back from the GPU and implement the forward process with the updated weights on the test image sets to get the accuracy of our model.
Milestones
Background
The advent of Machine learning and Deep Learning has revolutionized the technology industry. Deep Learning has played a great role in solving the handwritten digit recognition task and allowed many to achieve near state of the art performance. In this project, I will be using a GPU for recognizing handwritten digits using a neural network. In the past, many have succeeded in reaching an error rate of 0.42% and 0.17%. I too will be aiming at such numbers. Upon doing some online reading, I found that people have primarily approached the problem using the following: a Multi-Layer Perceptron and a Parallel Multi-Layer Neural Network.
The first approach is implementing a Multi-Layer Perceptron Neural Network. A Multi-Layer Perceptron Neural Network (also called Feed Forward Supervised Neural Network) consists of three parts: Input Layer, Hidden Layers and an Output Layer. Each layer is made up of nodes which are called Neurons which connect to other neurons in the network. The activation function of each of the nodes in the sigmoid function:
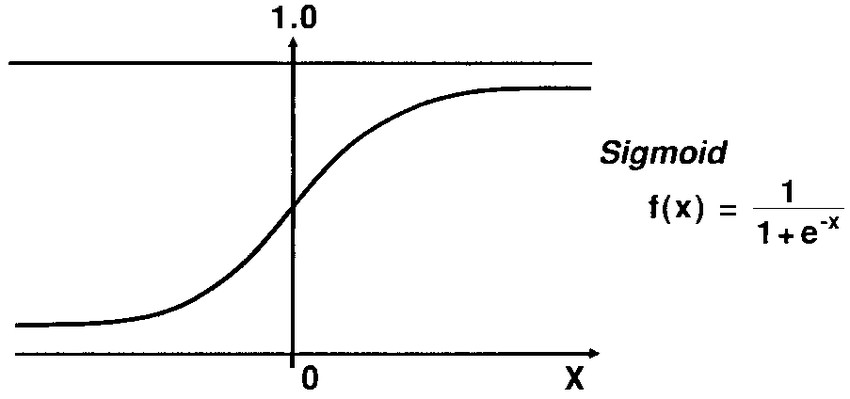
The Neural Network minimizes the cost function using gradient descent to update the weights and biases.
In order to parallelize the training of the Multi-Layer Perceptron Neural Network(MLP), I came up with the following ideas:
Forward Propagation: Parallelize the matrix multiplication at each layer. An example is node parallelism where threads are assigned to nodes of a neural network. Each thread handles the weight updates and activations for its respective node: http://www.cs.otago.ac.nz/staffpriv/hzy/papers/pdcs03.pdf
Backward Propagation: Update weights in parallel since they are independent. Implement tiled matrix multiplications: http://www-scf.usc.edu/~nkamra/pdf/pgd.pdf
Implementation
Non-optimized parallel code time: 5989.67 ms
For the implementation of my fully connected neural network, I followed the source of the sequential code and chose a neural network architecture consisting of three layers with 784 neurons in the first layer since the input images are 32 x 32, 128 neurons in the second layer, 10 neurons for the third layer with each neuron corresponding to each number from 1 to 9. I developed in total, four kernels to compute the process of the input image going through the forward propagation through the neural network and then the backward propagation to update the weights of the neural network.
For forward propagation, I implemented one kernel and for backward propagation, I implemented three kernels. For forward propagation, I implemented two matrix vector multiplication representing the input vector propagating through the neural network and being multiplied by the weights. The weights of my neural network are represented by two weight matrices, the first one representing the weights between layer 1 and layer 2 and the second one representing the weights between layer 2 and layer 3. For forward propagation, I allocated the same number of threads as the size of the second layer which was 128 in my case. Each thread was then mapped to each element of the output vectors based on its thread index to compute the output element.
For backpropagation, I used three kernels. The first kernel was used to compute the gradient of the loss function with respect to the outputs of each layer. And the other two kernels were used to compute the gradient of the loss function with respect to the weights using the output from the first kernel and chain rule. One of the two kernels computed the gradients and updated weights between layer 1 and layer 2 and the other kernel computed gradients and updated the weights between layer 2 and layer 3. For the first kernel, I allocated the same number of threads as the size of the second layer which was 128 and each thread computed the gradient of the loss with respect to the outputs of layer 2 and layer 3 based on its thread index. For the last two kernels, I allocated the same number of threads as the number of weights the kernel was updating and had each thread compute the gradient with respect to the weight mapping to its index and update it. This process was repeated for the entire training data where looping through the training data was done in the host. Throughout my implementation, I was careful to minimize my use of memory, allocating a minimum number of threads necessary, minimizing global memory access.
Optimizations
The parallel code from above took 5989.67 ms to train and compute the output labels and so I decided to implement the following optimizations:
1. Tiled-Matrix Multiplication: In the original code, each thread was computing its corresponding output in the output vector for each layer. If the weight vectors and input vector were really huge this would not be optimal. In that case, I can use tiled matrix multiplication where I bring parts of the weight matrices and input vector into shared memory and do my computations reducing global memory access.
To bring down the global memory accesses, I used Tiled Matrix Multiplication in the forward propagation kernel (perceptron), where I bring parts of the weight matrices and input vector into shared memory.
Computation Time: 3167.28 ms
Accuracy: 93.71%
2. Better Memory Coalescing: Accessing weight matrices in row-major order led to poor memory coalescing but using column-major order to access the weights improved computation time, a lot. I did this for all the kernels I implemented along with the sequential initialization code in wrapper function.
Computation Time: 2956.39 ms
Accuracy: 94.16%
3. Utilizing shared memory: Some of the data such as the weights and deltas are reused across kernel invocations. I thought it’s possible to keep some of them inside shared memory if they are not too large thus reducing global memory access. Constant values such as learning rate and momentum can be kept in constant memory of the kernels.
Computation Time: 2947.14 ms
Accuracy: 94.16%
4. Using Streams: I realized that the two kernels in backpropagation part 2 (back_propagation_2_w1 and back_propagation_2_w2) can be parallelized as they are independent. I tried to implement this by using 2 Cuda Streams. But when implemented this actually gave slightly poorer results so I decided against it.
Computation Time: 2998.79 ms
Accuracy: 94.16%
Note:- All the above measurements are for a 1 epoch training run. In our submitted code we use 2 epochs to train for better accuracy. For the submitted code computation time is 5873.07 ms with 95.1% accuracy.
Results
In the end, I was able to achieve an accuracy of 95.1% and our code took 5873.07 ms computation time. I had trained on 60,000 images and used 10,000 images for testing and of those test images, 9510 were identified correctly by our Neural Network. The sequential code took 274 minutes whereas ours took 5873.07 ms (5.87 s approx). Our parallel code was about 2800 times faster than the sequential code. We trained for 2 epochs so training time per epoch on average is 2936.54 ms (3s approx).
Conclusion
This project made me realize that Parallel Programming truly is easy if you do not care about performance. There are a lot of components that are independent and can be parallelized in the code for Neural Networks. It certainly helped that I was given the sequential code because we were able to build our parallel version off of it and that version did very well in terms of computation time and accuracy. At first glance, it was very easy to see that backpropagation and forward propagation could be implemented in parallel. However, it took us some thinking to realize that we can use shared memory and use better memory coalescing to improve computation time. Overall, Neural Networks have great potential to be parallelized and are very fast when implemented on GPUs.
Reference
- Y. Liu, W. Jing, and L. Xu, “Parallelizing Backpropagation Neural Network Using MapReduce and Cascading Model,” Computational Intelligence and Neuroscience, vol. 2016, pp. 1–11, 2016.
Retrieved from: https://www.hindawi.com/journals/cin/2016/2842780/
- M. Pethick, M. Liddle, P. Werstein, and Z. Huang, “Parallelization of a Backpropagation Neural Network on a Cluster Computer,” University of Otago.
Retrieved from: http://www.cs.otago.ac.nz/staffpriv/hzy/papers/pdcs03.pdf
- N. Kamra, P. Goyal, S. Seo, and V. Zois, “Parallel Gradient Descent for Multilayer Feedforward Neural Networks,” University of Southern California.
Retrieved from: http://www-scf.usc.edu/~nkamra/pdf/pgd.pdf
- A. Haghrah, “Simple MLP Backpropagation Artificial Neural Network in C++”
Retrieved from: https://www.codeproject.com/Articles/126/Simple-MLP-Backpropagation-Artificial-Neural-Netwo
- D. Hunter, and B. Wilamowski, “Parallel Multi-Layer Neural Network Architecture with Improved Efficiency”, Auburn University.
Retrieved from: http://www.eng.auburn.edu/~wilambm/pap/2011/Parallel%20Multi-layer%20NN.pdf